The goal of this chapter is to show how the Poisson equation, the most basic of all PDEs, can be quickly solved with a few lines of FEniCS code. We introduce the most fundamental FEniCS objects such asMesh,Function,FunctionSpace,TrialFunction, andTestFunction, and learn how to write a basic PDE solver, including how to formulate the mathematical variational problem, apply boundary conditions, call the FEniCS solver, and plot the solution.
Many books on programming languages start with a “Hello, World!” program. Readers are curious to know how fundamental tasks are expressed in the language, and printing a text to the screen can be such a task. In the world of finite element methods for PDEs, the most fundamental task must be to solve the Poisson equation. Our counterpart to the classical “Hello, World!” program therefore solves the following boundary-value problem:
Here, \(u = u(\boldsymbol{x})\) is the unknown function, \(f = f(\boldsymbol{x})\) is a prescribed function, \(\nabla^2\) is the Laplace operator (often written as \(\Delta\)), \(\Omega\) is the spatial domain, and \(\partial\Omega\) is the boundary of \(\Omega\). The Poisson problem, including both the PDE \(-\nabla^2 u = f\) and the boundary condition \(u = u_{_\mathrm{D}}\) on \(\partial \Omega\), is an example of a boundary-value problem, which must be precisely stated before it makes sense to start solving it with FEniCS.
In two space dimensions with coordinates \(x\) and \(y\), we can write out the Poisson equation as
The unknown \(u\) is now a function of two variables, \(u = u(x,y)\), defined over a two-dimensional domain \(\Omega\).
The Poisson equation arises in numerous physical contexts, including heat conduction, electrostatics, diffusion of substances, twisting of elastic rods, inviscid fluid flow, and water waves. Moreover, the equation appears in numerical splitting strategies for more complicated systems of PDEs, in particular the Navier - Stokes equations.
Solving a boundary-value problem such as the Poisson equation in FEniCS consists of the following steps:
- Identify the computational domain (\(\Omega\)), the PDE, its boundary conditions, and source terms (\(f\)).
- Reformulate the PDE as a finite element variational problem.
- Write a Python program which defines the computational domain, the variational problem, the boundary conditions, and source terms, using the corresponding FEniCS abstractions.
- Call FEniCS to solve the boundary-value problem and, optionally, extend the program to compute derived quantities such as fluxes and averages, and visualize the results.
We shall now go through steps 2 - 4 in detail. The key feature of FEniCS is that steps 3 and 4 result in fairly short code, while a similar program in most other software frameworks for PDEs require much more code and technically difficult programming.
What makes FEniCS attractive
Although many software frameworks have a really elegant “Hello, World!” example for the Poisson equation, FEniCS is to our knowledge the only framework where the code stays compact and nice, very close to the mathematical formulation, even when the mathematical and algorithmic complexity increases and when moving from a laptop to a high-performance compute server (cluster).
FEniCS is based on the finite element method, which is a general and efficient mathematical machinery for the numerical solution of PDEs. The starting point for the finite element methods is a PDE expressed in variational form. Readers who are not familiar with variational problems will get a very brief introduction to the topic in this tutorial, but reading a proper book on the finite element method in addition is encouraged. The section The finite element method contains a list of recommended books. Experience shows that you can work with FEniCS as a tool to solve PDEs even without thorough knowledge of the finite element method, as long as you get somebody to help you with formulating the PDE as a variational problem.
The basic recipe for turning a PDE into a variational problem is to multiply the PDE by a function \(v\), integrate the resulting equation over the domain \(\Omega\), and perform integration by parts of terms with second-order derivatives. The function \(v\) which multiplies the PDE is called a test function. The unknown function \(u\) to be approximated is referred to as a trial function. The terms trial and test functions are used in FEniCS programs too. The trial and test functions belong to certain so-called function spaces that specify the properties of the functions.
In the present case, we first multiply the Poisson equation by the test function \(v\) and integrate over \(\Omega\):
We here let \({\, \mathrm{d}x}\) denote the differential element for integration over the domain \(\Omega\). We will later let \({\, \mathrm{d}s}\) denote the differential element for integration over the boundary of \(\Omega\).
A common rule when we derive variational formulations is that we try to keep the order of the derivatives of \(u\) and \(v\) as small as possible. Here, we have a second-order spatial derivative of \(u\), which can be transformed to a first-derivative of \(u\) and \(v\) by applying the technique of integration by parts. The formula reads
where \(\frac{\partial u}{\partial n} = \nabla u \cdot n\) is the derivative of \(u\) in the outward normal direction \(n\) on the boundary.
Another feature of variational formulations is that the test function \(v\) is required to vanish on the parts of the boundary where the solution \(u\) is known (the book [Ref14] explains in detail why this requirement is necessary). In the present problem, this means that \(v=0\) on the whole boundary \(\partial\Omega\). The second term on the right-hand side of (5) therefore vanishes. From (4) and (5) it follows that
If we require that this equation holds for all test functions \(v\) in some suitable space \(\hat V\), the so-called test space, we obtain a well-defined mathematical problem that uniquely determines the solution \(u\) which lies in some (possibly different) function space \(V\), the so-called trial space. We refer to (6) as the weak form or variational form of the original boundary-value problem (1)–(2).
The proper statement of our variational problem now goes as follows: find \(u \in V\) such that
The trial and test spaces \(V\) and \(\hat V\) are in the present problem defined as
In short, \(H^1(\Omega)\) is the mathematically well-known Sobolev space containing functions \(v\) such that \(v^2\) and \(|\nabla v|^2\) have finite integrals over \(\Omega\) (essentially meaning that the functions are continuous). The solution of the underlying PDE must lie in a function space where the derivatives are also continuous, but the Sobolev space \(H^1(\Omega)\) allows functions with discontinuous derivatives. This weaker continuity requirement of \(u\) in the variational statement (7), as a result of the integration by parts, has great practical consequences when it comes to constructing finite element function spaces. In particular, it allows the use of piecewise polynomial function spaces; i.e., function spaces constructed by stitching together polynomial functions on simple domains such as intervals, triangles, or tetrahedrons.
The variational problem (7) is a continuous problem: it defines the solution \(u\) in the infinite-dimensional function space \(V\). The finite element method for the Poisson equation finds an approximate solution of the variational problem (7) by replacing the infinite-dimensional function spaces \(V\) and \(\hat{V}\) by discrete (finite-dimensional) trial and test spaces \(V_h\subset{V}\) and \(\hat{V}_h\subset\hat{V}\). The discrete variational problem reads: find \(u_h \in V_h \subset V\) such that
This variational problem, together with a suitable definition of the function spaces \(V_h\) and \(\hat{V}_h\), uniquely define our approximate numerical solution of Poisson’s equation (1). Note that the boundary conditions are encoded as part of the trial and test spaces. The mathematical framework may seem complicated at first glance, but the good news is that the finite element variational problem (8) looks the same as the continuous variational problem (7), and FEniCS can automatically solve variational problems like (8)!
What we mean by the notation \(u\) and \(V\)
The mathematics literature on variational problems writes \(u_h\) for the solution of the discrete problem and \(u\) for the solution of the continuous problem. To obtain (almost) a one-to-one relationship between the mathematical formulation of a problem and the corresponding FEniCS program, we shall drop the subscript \(_h\) and use \(u\) for the solution of the discrete problem. We will use \({u_{\small\mbox{e}}}\) for the exact solution of the continuous problem, if we need to explicitly distinguish between the two. Similarly, we will let \(V\) denote the discrete finite element function space in which we seek our solution.
It turns out to be convenient to introduce the following canonical notation for variational problems: find \(u\in V\) such that
For the Poisson equation, we have:
From the mathematics literature, \(a(u,v)\) is known as a bilinear form and \(L(v)\) as a linear form. We shall, in every linear problem we solve, identify the terms with the unknown \(u\) and collect them in \(a(u,v)\), and similarly collect all terms with only known functions in \(L(v)\). The formulas for \(a\) and \(L\) can then be expressed directly in our FEniCS programs.
To solve a linear PDE in FEniCS, such as the Poisson equation, a user thus needs to perform only two steps:
- Choose the finite element spaces \(V\) and \(\hat V\) by specifying the domain (the mesh) and the type of function space (polynomial degree and type).
- Express the PDE as a (discrete) variational problem: find \(u\in V\) such that \(a(u,v) = L(v)\) for all \(v\in \hat{V}\).
The Poisson problem (1)–(2) has so far featured a general domain \(\Omega\) and general functions \(u_{_\mathrm{D}}\) for the boundary conditions and \(f\) for the right-hand side. For our first implementation we will need to make specific choices for \(\Omega\), \(u_{_\mathrm{D}}\), and \(f\). It will be wise to construct a problem with a known analytical solution so that we can easily check that the computed solution is correct. Solutions that are lower-order polynomials are primary candidates. Standard finite element function spaces of degree \(r\) will exactly reproduce polynomials of degree \(r\). And piecewise linear elements (\(r=1\)) are able to exactly reproduce a quadratic polynomial on a uniformly partitioned mesh. This important result can be used to verify our implementation. We just manufacture some quadratic function in 2D as the exact solution, say
By inserting (12) into the Poisson equation (1), we find that \({u_{\small\mbox{e}}}(x,y)\) is a solution if
regardless of the shape of the domain as long as \({u_{\small\mbox{e}}}\) is prescribed along the boundary. We choose here, for simplicity, the domain to be the unit square,
This simple but very powerful method for constructing test problems is called the method of manufactured solutions: pick a simple expression for the exact solution, plug it into the equation to obtain the right-hand side (source term \(f\)), then solve the equation with this right-hand side and using the exact solution as a boundary condition, and try to reproduce the exact solution.
Tip: Try to verify your code with exact numerical solutions
A common approach to testing the implementation of a numerical method is to compare the numerical solution with an exact analytical solution of the test problem and conclude that the program works if the error is “small enough”. Unfortunately, it is impossible to tell if an error of size \(10^{-5}\) on a \(20\times 20\) mesh of linear elements is the expected (in)accuracy of the numerical approximation or if the error also contains the effect of a bug in the code. All we usually know about the numerical error is its asymptotic properties, for instance that it is proportional to \(h^2\) if \(h\) is the size of a cell in the mesh. Then we compare the error on meshes with different \(h\)-values to see if the asymptotic behavior is correct. This is a very powerful verification technique and is explained in detail in the section Computing convergence rates (1). However, if we have a test problem for which we know that there should be no approximation errors, we know that the analytical solution of the PDE problem should be reproduced to machine precision by the program. That is why we emphasize this kind of test problems throughout this tutorial. Typically, elements of degree \(r\) can reproduce polynomials of degree \(r\) exactly, so this is the starting point for constructing a solution without numerical approximation errors.
A FEniCS program for solving our test problem for the Poisson equation in 2D with the given choices of \(\Omega\), \(u_{_\mathrm{D}}\), and \(f\) may look as follows:
from fenics import *
# Create mesh and define function space
mesh = UnitSquareMesh(8, 8)
V = FunctionSpace(mesh, 'P', 1)
# Define boundary condition
u_D = Expression('1 + x[0]*x[0] + 2*x[1]*x[1]', degree=2)
def boundary(x, on_boundary):
return on_boundary
bc = DirichletBC(V, u_D, boundary)
# Define variational problem
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(-6.0)
a = dot(grad(u), grad(v))*dx
L = f*v*dx
# Compute solution
u = Function(V)
solve(a == L, u, bc)
# Plot solution and mesh
plot(u)
plot(mesh)
# Save solution to file in VTK format
vtkfile = File('poisson/solution.pvd')
vtkfile << u
# Compute error in L2 norm
error_L2 = errornorm(u_D, u, 'L2')
# Compute maximum error at vertices
vertex_values_u_D = u_D.compute_vertex_values(mesh)
vertex_values_u = u.compute_vertex_values(mesh)
import numpy as np
error_max = np.max(np.abs(vertex_values_u_D - vertex_values_u))
# Print errors
print('error_L2 =', error_L2)
print('error_max =', error_max)
# Hold plot
interactive()
This example program can be found in the file ft01_poisson.py.
The FEniCS program must be available in a plain text file, written with a text editor such as Atom, Sublime Text, Emacs, Vim, or similar. There are several ways to run a Python program like ft01_poisson.py:
- Use a terminal window.
- Use an integrated development environment (IDE), e.g., Spyder.
- Use a Jupyter notebook.
Open a terminal window, move to the directory containing the program and type the following command:
Terminal> python ft01_poisson.py
Note that this command must be run in a FEniCS-enabled terminal. For
users of the FEniCS Docker containers, this means that you must type
this command after you have started a FEniCS session using
fenicsproject run or fenicsproject start.
When running the above command, FEniCS will run the program to compute the approximate solution \(u\). The approximate solution \(u\) will be compared to the exact solution \({u_{\small\mbox{e}}} = u_{_\mathrm{D}}\) and the error in the \(L^2\) and maximum norms will be printed. Since we know that our approximate solution should reproduce the exact solution to within machine precision, this error should be small, something on the order of \(10^{-15}\). If plotting is enabled in your FEniCS installation, then a window with a simple plot of the solution will appear as in Figure Plot of the mesh and the solution for the Poisson problem created using the built-in FEniCS visualization tool (``plot`` command).
Many prefer to work in an integrated development environment that provides an editor for programming, a window for executing code, a window for inspecting objects, etc. Just open the file ft01_poisson.py and press the play button to run it. We refer to the Spyder tutorial to learn more about working in the Spyder environment. Spyder is highly recommended if you are used to working in the graphical MATLAB environment.
Notebooks make it possible to mix text and executable code in the same
document, but you can also just use it to run programs in a web
browser. Run the command jupyter notebook from a terminal window,
find the New pulldown menu in the upper right corner of the GUI,
choose a new notebook in Python 2 or 3, write %load
ft01_poisson.py in the blank cell of this notebook, then press
Shift+Enter to execute the cell. The file ft01_poisson.py will then be loaded into the
notebook. Re-execute the cell (Shift+Enter) to run the program. You
may divide the entire program into several cells to examine
intermediate results: place the cursor where you want to split the
cell and choose Edit - Split Cell. For users of the FEniCS Docker
images, run the fenicsproject notebook command and follow the
instructions. To enable plotting, make sure to run the command
%matplotlib inline inside the notebook.
We shall now dissect our FEniCS program in detail. The listed FEniCS
program defines a finite element mesh, a finite element function space
\(V\) on this mesh, boundary conditions for \(u\) (the function \(u_{_\mathrm{D}}\)),
and the bilinear and linear forms \(a(u,v)\) and \(L(v)\). Thereafter, the
solution \(u\) is computed. At the end of the program, we compare the
numerical and the exact solutions. We also plot the solution using the
plot command and save the solution to a file for external
postprocessing.
The first line in the program,
from fenics import *
imports the key classes UnitSquareMesh, FunctionSpace, Function,
and so forth, from the FEniCS library. All FEniCS programs for
solving PDEs by the finite element method normally start with this
line.
The statement
mesh = UnitSquareMesh(8, 8)
defines a uniform finite element mesh over the unit square \([0,1]\times [0,1]\). The mesh consists of cells, which in 2D are triangles with straight sides. The parameters 8 and 8 specify that the square should be divided into \(8\times 8\) rectangles, each divided into a pair of triangles. The total number of triangles (cells) thus becomes 128. The total number of vertices in the mesh is \(9\cdot 9=81\). In later chapters, you will learn how to generate more complex meshes.
Once the mesh has been created, we can create a finite element
function space V:
V = FunctionSpace(mesh, 'P', 1)
The second argument 'P' specifies the type of element. The type of
element here is \(\mathsf{P}\), implying the standard Lagrange family of
elements. You may also use 'Lagrange' to specify this type of
element. FEniCS supports all simplex element families and the notation
defined in the Periodic Table of the Finite Elements [Ref26].
The third argument 1 specifies the degree of the finite element. In
this case, the standard \(\mathsf{P}_1\) linear Lagrange element, which
is a triangle with nodes at the three vertices. Some finite element
practitioners refer to this element as the “linear triangle”. The
computed solution \(u\) will be continuous across elements and linearly
varying in \(x\) and \(y\) inside each element. Higher-degree polynomial
approximations over each cell are trivially obtained by increasing the
third parameter to FunctionSpace, which will then generate function
spaces of type \(\mathsf{P}_2\), \(\mathsf{P}_3\), and so forth. Changing
the second parameter to 'DP' creates a function space for
discontinuous Galerkin methods.
In mathematics, we distinguish between the trial and test spaces \(V\)
and \(\hat{V}\). The only difference in the present problem is the
boundary conditions. In FEniCS we do not specify the boundary
conditions as part of the function space, so it is sufficient to work
with one common space V for both the trial and test functions in the
program:
u = TrialFunction(V)
v = TestFunction(V)
The next step is to specify the boundary condition: \(u=u_{_\mathrm{D}}\) on \(\partial\Omega\). This is done by
bc = DirichletBC(V, u_D, boundary)
where u_D is an expression defining the solution values on the
boundary, and boundary is a function (or object) defining
which points belong to the boundary.
Boundary conditions of the type \(u=u_{_\mathrm{D}}\) are known as Dirichlet
conditions. For the present finite element method for the Poisson
problem, they are also called essential boundary conditions, as they
need to be imposed explicitly as part of the trial space (in contrast
to being defined implicitly as part of the variational formulation).
Naturally, the FEniCS class used to define Dirichlet boundary
conditions is named DirichletBC.
The variable u_D refers to an Expression object, which is used to
represent a mathematical function. The typical construction is
u_D = Expression(formula, degree=1)
where formula is a string containing a mathematical expression.
The formula must be written with C++ syntax and is
automatically turned into an efficient, compiled C++ function.
Expressions and accuracy
When defining an Expression, the second argument degree is a
parameter that specifies how the expression should be treated in
computations. On each local element, FEniCS will interpolate the
expression into a finite element space
of the specified degree. To obtain optimal
(order of) accuracy in computations, it is usually a good choice to
use the same degree as for the space \(V\) that is used for the trial
and test functions. However, if an Expression is used to represent
an exact solution which is used to evaluate the accuracy of a computed
solution, a higher degree must be used for the expression (one or two
degrees higher).
The expression may depend on the variables x[0] and x[1]
corresponding to the \(x\) and \(y\) coordinates. In 3D, the expression
may also depend on the variable x[2] corresponding to the \(z\)
coordinate. With our choice of \(u_{_\mathrm{D}}(x,y)=1 + x^2 + 2y^2\), the formula
string can be written as 1 + x[0]*x[0] + 2*x[1]*x[1]:
u_D = Expression('1 + x[0]*x[0] + 2*x[1]*x[1]', degree=2)
We set the degree to \(2\) so that u_D may represent the exact
quadratic solution to our test problem.
String expressions must have valid C++ syntax
The string argument to an Expression object must obey C++ syntax.
Most Python syntax for mathematical expressions is also valid C++ syntax,
but power expressions make an exception: p**a must be written as
pow(p, a) in C++ (this is also an alternative Python syntax).
The following mathematical functions can be used directly
in C++
expressions when defining Expression objects:
cos, sin, tan, acos, asin,
atan, atan2, cosh, sinh, tanh, exp,
frexp, ldexp, log, log10, modf,
pow, sqrt, ceil, fabs, floor, and fmod.
Moreover, the number \(\pi\) is available as the symbol pi.
All the listed functions are taken from the cmath C++ header file, and
one may hence
consult the documentation of cmath for more information on the
various functions.
If/else tests are possible using the C syntax for inline branching. The function
is implemented as
f = Expression('x[0]>=0 && x[1]>=0 ? pow(x[0], 2) : 2', degree=2)
Parameters in expression strings are allowed, but
must be initialized via keyword
arguments when creating the Expression object. For example, the
function \(f(x)=e^{-\kappa\pi^2t}\sin(\pi k x)\) can be coded as
f = Expression('exp(-kappa*pow(pi, 2)*t)*sin(pi*k*x[0])', degree=2,
kappa=1.0, t=0, k=4)
At any time, parameters can be updated:
f.t += dt
f.k = 10
The function boundary specifies which points that belong to the
part of the boundary where the boundary condition should be applied:
def boundary(x, on_boundary):
return on_boundary
A function like boundary for marking the boundary must return a
boolean value: True if the given point x lies on the Dirichlet
boundary and False otherwise. The argument on_boundary is True
if x is on the physical boundary of the mesh, so in the present
case, where we are supposed to return True for all points on the
boundary, we can just return the supplied value of on_boundary. The
boundary function will be called for every discrete point in the
mesh, which means that we may define boundaries where \(u\) is also
known inside the domain, if desired.
One way to think about the specification of boundaries in FEniCS is
that FEniCS will ask you (or rather the function boundary which
you have implemented) whether or not a specific point x is part of
the boundary. FEniCS already knows whether the point belongs to the
actual boundary (the mathematical boundary of the domain) and kindly
shares this information with you in the variable on_boundary. You
may choose to use this information (as we do here), or ignore it
completely.
The argument on_boundary may also be omitted, but in that case we need
to test on the value of the coordinates in x:
def boundary(x):
return x[0] == 0 or x[1] == 0 or x[0] == 1 or x[1] == 1
Comparing floating-point values using an exact match test with
== is not good programming practice, because small round-off errors
in the computations of the x values could make a test x[0] == 1
become false even though x lies on the boundary. A better test is
to check for equality with a tolerance, either explicitly
tol = 1E-14
def boundary(x):
return abs(x[0]) < tol or abs(x[1]) < tol \
or abs(x[0] - 1) < tol or abs(x[1] - 1) < tol
or using the near command in FEniCS:
def boundary(x):
return near(x[0], 0, tol) or near(x[1], 0, tol) \
or near(x[0], 1, tol) or near(x[1], 1, tol)
Never use == for comparing real numbers
A comparison like x[0] == 1 should never be used if x[0] is a real
number, because rounding errors in x[0] may make the test fail even
when it is mathematically correct. Consider the following calculations
in Python:
>>> 0.1 + 0.2 == 0.3
False
>>> 0.1 + 0.2
0.30000000000000004
Comparison of real numbers needs to be made with tolerances! The values of the tolerances depend on the size of the numbers involved in arithmetic operations:
>>> abs(0.1 + 0.2 - 0.3)
5.551115123125783e-17
>>> abs(1.1 + 1.2 - 2.3)
0.0
>>> abs(10.1 + 10.2 - 20.3)
3.552713678800501e-15
>>> abs(100.1 + 100.2 - 200.3)
0.0
>>> abs(1000.1 + 1000.2 - 2000.3)
2.2737367544323206e-13
>>> abs(10000.1 + 10000.2 - 20000.3)
3.637978807091713e-12
For numbers of unit size, tolerances as low as \(3\cdot 10^{-16}\) can be used
(in fact, this tolerance is known as the constant DOLFIN_EPS in FEniCS).
Otherwise, an appropriately scaled tolerance must be used.
Before defining the bilinear and linear forms \(a(u,v)\) and \(L(v)\) we have to specify the source term \(f\):
f = Expression('-6', degree=0)
When \(f\) is constant over the domain, f can be
more efficiently represented as a Constant:
f = Constant(-6)
We now have all the ingredients we need to define the variational problem:
a = dot(grad(u), grad(v))*dx
L = f*v*dx
In essence, these two lines specify the PDE to be solved. Note the very close correspondence between the Python syntax and the mathematical formulas \(\nabla u\cdot\nabla v {\, \mathrm{d}x}\) and \(fv {\, \mathrm{d}x}\). This is a key strength of FEniCS: the formulas in the variational formulation translate directly to very similar Python code, a feature that makes it easy to specify and solve complicated PDE problems. The language used to express weak forms is called UFL (Unified Form Language) [Ref05] [Ref01] and is an integral part of FEniCS.
Expressing inner products
The inner product \(\int_{\Omega} \nabla u \cdot \nabla v {\, \mathrm{d}x}\)
can be expressed in various ways in FEniCS. Above, we have used
the notation dot(grad(u), grad(v))*dx. The dot product in
FEniCS/UFL computes the sum (contraction) over the last index
of the first factor and the first index of the second factor.
In this case, both factors are tensors of rank one (vectors) and
so the sum is just over the one single index of both \(\nabla u\)
and \(\nabla v\). To compute an inner product of matrices (with
two indices), one must instead of dot use the function inner.
For vectors, dot and inner are equivalent.
Having defined the finite element variational problem and boundary condition, we can now ask FEniCS to compute the solution:
u = Function(V)
solve(a == L, u, bc)
Note that we first defined the variable u as a TrialFunction and
used it to represent the unknown in the form a. Thereafter, we
redefined u to be a Function object representing the solution;
i.e., the computed finite element function \(u\). This redefinition of
the variable u is possible in Python and is often used in FEniCS
applications for linear problems. The two types of objects that u
refers to are equal from a mathematical point of view, and hence it is
natural to use the same variable name for both objects.
plot command¶Once the solution has been computed, it can be visualized by
the plot command:
plot(u)
plot(mesh)
interactive()
Note the call to the function interactive after the plot commands.
This call makes it possible to interact with the plots (rotating and
zooming). The call to interactive is usually placed at the end of a
program that creates plots. Figure Plot of the mesh and the solution for the Poisson problem created using the built-in FEniCS visualization tool (``plot`` command) displays the
two plots.
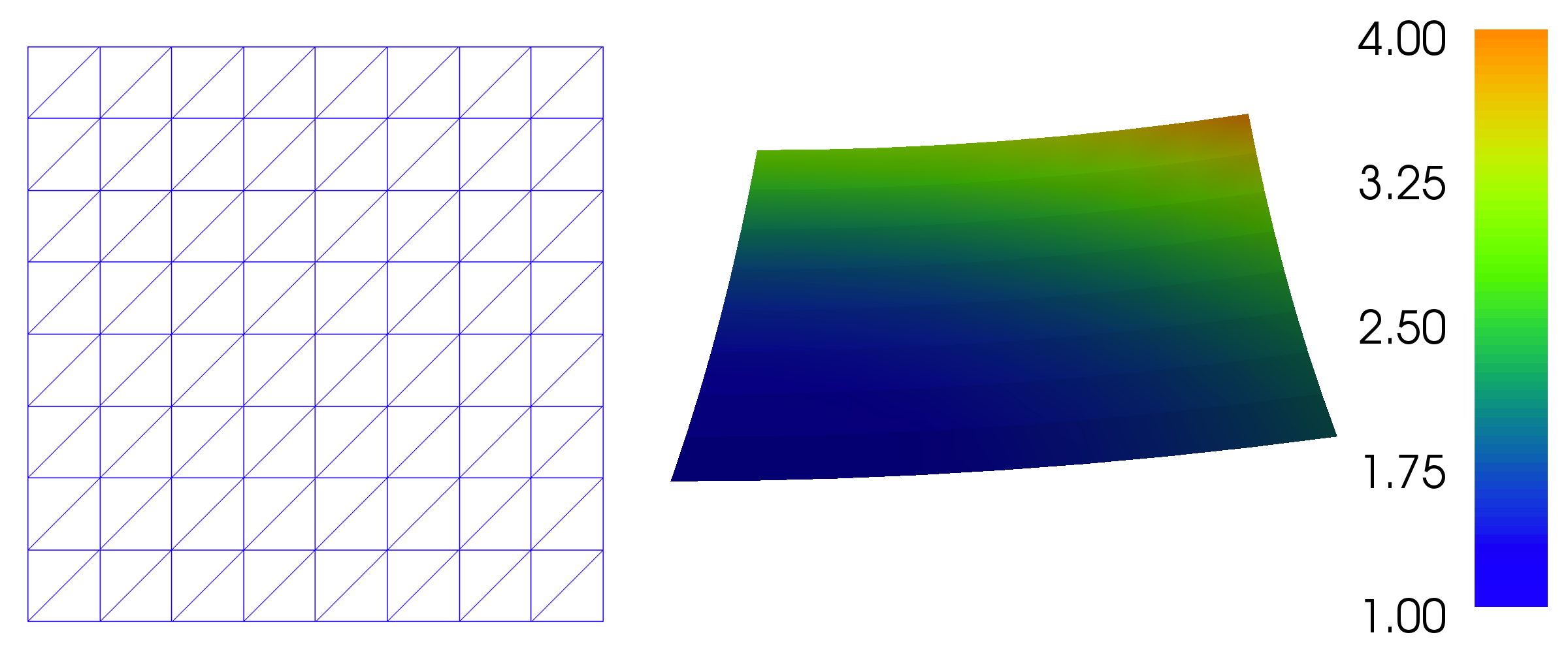
Plot of the mesh and the solution for the Poisson problem created using the built-in FEniCS visualization tool (``plot`` command)
The plot command is useful for debugging and initial scientific
investigations. More advanced visualizations are better created by
exporting the solution to a file and using an advanced visualization
tool like ParaView, as explained in the next section.
By clicking the left mouse button in the plot window, you may rotate
the solution, while the right mouse button is used for zooming. Point
the mouse to the Help text in the lower left corner to display a
list of all available shortcut commands. The help menu may
alternatively be activated by typing h in the plot window. The
plot command also accepts a number of additional arguments, such as
for example setting the title of the plot window:
plot(u, title='Finite element solution')
plot(mesh, title='Finite element mesh')
For detailed documentation, either run the command help(plot) in
Python or pydoc fenics.plot from a terminal window.
Built-in plotting on Mac OS X and in Docker
The built-in plotting in FEniCS may not work as expected when either
running on Mac OS X or when running inside a FEniCS Docker container.
FEniCS supports plotting using the plot command on Mac OS
X. However, the keyboard shortcuts may fail
to work. When running inside a Docker container, plotting is not
supported since Docker does not interact with your windowing system.
For Docker users who need plotting, it is recommended to either work
within a Jupyter/FEniCS notebook (command fenicsproject notebook)
or rely on ParaView or other external tools for visualization.
The simple plot command is useful for quick visualizations, but for
more advanced visualizations an external tool must be used. In this
section we demonstrate how to visualize solutions in ParaView.
ParaView is a powerful
tool for visualizing scalar and vector fields, including those
computed by FEniCS.
The first step is to export the solution in VTK format:
vtkfile = File('poisson/solution.pvd')
vtkfile << u
The following steps demonstrate how to create a plot of the solution of our Poisson problem in ParaView. The resulting plot is shown in Figure Plot of the mesh and the solution for the Poisson problem created using ParaView.
poisson below the directory where the FEniCS Python program was started. Select the file named solution.pvd and then click OK.solution.pvd in the Pipeline Browser pane on the left. Also click the little 2D button at the top of the plot window to change the visualization to 3D. This lets you interact with the plot by rotating (left mouse button) and zooming (Ctrl + left mouse button).solution.pvd in the Pipeline Browser, navigate to Representation in the Properties pane, and select Surface With Edges. This should make the finite element mesh visible.poisson.png.For more information, we refer to The ParaView Guide [Ref27] (free PDF available), the ParaView tutorial, and the instruction video Introduction to ParaView.
Finally, we compute the error to check the accuracy of the solution.
We do this by comparing the finite element solution u with the exact
solution, which in this example happens to be the same as the
expression u_D used to set the boundary conditions. We compute the
error in two different ways. First, we compute the \(L^2\) norm of the
error, defined by
Since the exact solution is quadratic and the finite element solution is piecewise linear, this error will be nonzero. To compute this error in FEniCS, we simply write
error_L2 = errornorm(u_D, u, 'L2')
The errornorm function can also compute other error norms such
as the \(H^1\) norm. Type pydoc fenics.errornorm in a terminal window
for details.
We also compute the maximum value of the error at all the vertices of
the finite element mesh. As mentioned above, we expect this error to
be zero to within machine precision for this particular example. To
compute the error at the vertices, we first ask FEniCS to compute the
value of both u_D and u at all vertices, and then subtract the
results:
vertex_values_u_D = u_D.compute_vertex_values(mesh)
vertex_values_u = u.compute_vertex_values(mesh)
import numpy as np
error_max = np.max(np.abs(vertex_values_u_D - vertex_values_u))
We have here used the maximum and absolute value functions from numpy,
because these are much more efficient for large arrays (a factor of 30)
than Python’s built-in max and abs functions.
How to check that the error vanishes
With inexact (floating point) arithmetic, the maximum error at the vertices is not zero, but should be a small number. The machine precision is about \(10^{-16}\), but in finite element calculations, rounding errors of this size may accumulate, to produce an error larger than \(10^{-16}\). Experiments show that increasing the number of elements and increasing the degree of the finite element polynomials increases the error. For a mesh with \(2\times(20\times 20)\) cubic Lagrange elements (degree 3) the error is about \(2\cdot 10^{-12}\), while for 128 linear elements the error is about \(2\cdot 10^{-15}\).
A finite element function like \(u\) is expressed as a linear combination of basis functions \(\phi_j\), spanning the space \(V\):
By writing solve(a == L, u, bc) in the program, a linear system will
be formed from \(a\) and \(L\), and this system is solved for the
values \(U_1,\ldots,U_N\). The values \(U_1,\ldots,U_N\) are known as the
degrees of freedom (“dofs”) or nodal values of \(u\). For Lagrange
elements (and many other element types) \(U_j\) is simply the value of
\(u\) at the node with global number \(j\). The locations of the nodes and
cell vertices coincide for linear Lagrange elements, while for
higher-order elements there are additional nodes associated with the
facets, edges and sometimes also the interior of cells.
Having u represented as a Function object, we can either evaluate
u(x) at any point x in the mesh (expensive operation!), or we can
grab all the degrees of freedom in the vector \(U\) directly by
nodal_values_u = u.vector()
The result is a Vector object, which is basically an encapsulation
of the vector object used in the linear algebra package that is used
to solve the linear system arising from the variational problem.
Since we program in Python it is convenient to convert the Vector
object to a standard numpy array for further processing:
array_u = nodal_values_u.array()
With numpy arrays we can write MATLAB-like code to analyze the
data. Indexing is done with square brackets: array_u[j], where the
index j always starts at 0. If the solution is computed with
piecewise linear Lagrange elements (\(\mathsf{P}_1\)), then the size of
the array array_u is equal to the number of vertices, and each
array_u[j] is the value at some vertex in the mesh. However, the degrees
of freedom are not necessarily numbered in the same way as the
vertices of the
mesh. (This is discussed in some detail in the section Examining the degrees of freedom).
If we therefore want to know the values at the vertices, we need to
call the function u.compute_vertex_values. This function returns
the values at all the vertices of the mesh as a numpy array with the same
numbering as for the vertices of the mesh, for example:
vertex_values_u = u.compute_vertex_values()
Note that for \(\mathsf{P}_1\) elements, the arrays array_u and vertex_values_u have the same lengths and contain the same values, albeit in different order.
Our first FEniCS program for the Poisson equation targeted a simple test problem where we could easily verify the implementation. We now turn our attention to a physically more relevant problem with solutions of somewhat more exciting shape.
We want to compute the deflection \(D(x,y)\) of a two-dimensional, circular membrane of radius \(R\), subject to a load \(p\) over the membrane. The appropriate PDE model is
Here, \(T\) is the tension in the membrane (constant), and \(p\) is the external pressure load. The boundary of the membrane has no deflection, implying \(D=0\) as a boundary condition. A localized load can be modeled as a Gaussian function:
The parameter \(A\) is the amplitude of the pressure, \((x_0,y_0)\) the localization of the maximum point of the load, and \(\sigma\) the “width” of \(p\). We will take the center \((x_0,y_0)\) of the pressure to be \((0, R_0)\) for some \(0 < R_0 < R\).
There are many physical parameters in this problem, and we can benefit from grouping them by means of scaling. Let us introduce dimensionless coordinates \(\bar x = x/R\), \(\bar y = y/R\), and a dimensionless deflection \(w=D/D_c\), where \(D_c\) is a characteristic size of the deflection. Introducing \(\bar R_0=R_0/R\), we obtain
where
With an appropriate scaling, \(w\) and its derivatives are of size unity, so the left-hand side of the scaled PDE is about unity in size, while the right-hand side has \(\alpha\) as its characteristic size. This suggest choosing \(\alpha\) to be unity, or around unity. We shall in this particular case choose \(\alpha=4\). (One can also find the analytical solution in scaled coordinates and show that the maximum deflection \(D(0,0)\) is \(D_c\) if we choose \(\alpha=4\) to determine \(D_c\).) With \(D_c=AR^2/(8\pi\sigma T)\) and dropping the bars we obtain the scaled problem
to be solved over the unit disc with \(w=0\) on the boundary. Now there are only two parameters to vary: the dimensionless extent of the pressure, \(\beta\), and the localization of the pressure peak, \(R_0\in [0,1]\). As \(\beta\rightarrow 0\), the solution will approach the special case \(w=1-x^2-y^2\).
Given a computed scaled solution \(w\), the physical deflection can be computed by
Just a few modifications are necessary to our previous program to solve this new problem.
A mesh over the unit disk can be created by the mshr tool in
FEniCS:
from mshr import *
domain = Circle(Point(0, 0), 1)
mesh = generate_mesh(domain, 64)
The Circle shape from mshr takes the center and radius of the
circle as arguments. The second argument to the generate_mesh
function specifies the desired mesh resolution. The cell size will be
(approximately) equal to the diameter of the domain divided by the
resolution.
The right-hand side pressure function
is represented by an Expression object. There
are two physical parameters in the formula for \(f\) that enter the
expression string and these parameters must have their values set
by keyword arguments:
beta = 8
R0 = 0.6
p = Expression('4*exp(-pow(beta, 2)*(pow(x[0], 2) + pow(x[1] - R0, 2)))',
degree=1, beta=beta, R0=R0)
The coordinates in Expression objects are always an array
x with components x[0], x[1], and x[2], corresponding to
\(x\), \(y\), and \(z\).
Otherwise we are free to introduce names of parameters as long as
these are given default values by keyword arguments. All the
parameters initialized by keyword arguments can at any time have their
values modified. For example, we may set
p.beta = 12
p.R0 = 0.3
The variational problem is the same as in
our first Poisson problem, but we may introduce w instead of u as
primary unknown and p instead of f as right-hand side function:
w = TrialFunction(V)
v = TestFunction(V)
a = dot(grad(w), grad(v))*dx
L = p*v*dx
w = Function(V)
solve(a == L, w, bc)
It is of interest to visualize the pressure \(p\) along with the
deflection \(w\) so that we may examine the membrane’s response to the
pressure. We must then transform the formula (Expression) to a
finite element function (Function). The most natural approach is to
construct a finite element function whose degrees of freedom are
calculated from \(p\). That is, we interpolate \(p\) to the function space
\(V\):
p = interpolate(p, V)
Note that the assignment to p destroys the previous Expression
object p, so if it is of interest to still have access to this
object, another name must be used for the Function object returned
by interpolate. The two functions w and p may be plotted
using the built-in plot command:
plot(w, title='Deflection')
plot(p, title='Load')
As before, we also export the solutions in VTK format for visualization in ParaView:
vtkfile_w = File('poisson_membrane/deflection.pvd')
vtkfile_w << w
vtkfile_p = File('poisson_membrane/load.pvd')
vtkfile_p << p
Figure Plot of the deflection (left) and load (right) for the membrane problem created using ParaView. The plot uses 10 equispaced isolines for the solution values and the optional jet colormap shows a visualization
of the deflection w and the load p created with ParaView.
Another way to compare the deflection and the load is to make a curve plot
along the line \(x=0\). This is just a matter of defining a set of points
along the \(y\)-axis and evaluating the finite element functions w and p
at these points:
# Curve plot along x = 0 comparing p and w
import numpy as np
import matplotlib.pyplot as plt
tol = 0.001 # avoid hitting points outside the domain
y = np.linspace(-1 + tol, 1 - tol, 101)
points = [(0, y_) for y_ in y] # 2D points
w_line = np.array([w(point) for point in points])
p_line = np.array([p(point) for point in points])
plt.plot(y, 50*w_line, 'k', linewidth=2) # magnify w
plt.plot(y, p_line, 'b--', linewidth=2)
plt.grid(True)
plt.xlabel('$y$')
plt.legend(['Deflection ($\\times 50$)', 'Load'], loc='upper left')
plt.savefig('poisson_membrane/curves.pdf')
plt.savefig('poisson_membrane/curves.png')
This example program can be found in the file ft02_poisson_membrane.py.
The resulting curve plot is shown in Figure Plot of the deflection and load for the membrane problem created using Matplotlib and sampling of the two functions along the \( y \) -axsis. The localized input (\(p\)) is heavily damped and smoothed in the output (\(w\)). This reflects a typical property of the Poisson equation.