21. Stokes equations with Taylor-Hood elements¶
This demo is implemented in a single Python file,
demo_stokes-taylorhood.py, which contains both the
variational form and the solver.
This demo illustrates how to:
- Read mesh and subdomains from file
- Use mixed function spaces
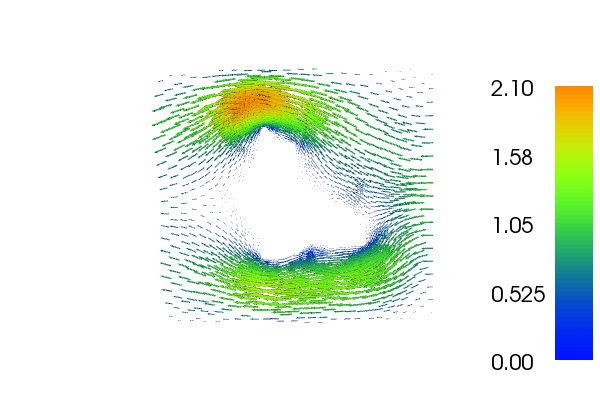
The mesh and subdomains look as follows:


and the solution of u and p, respectively:

21.1. Equation and problem definition¶
21.1.1. Strong formulation¶
Note
The sign of the pressure has been flipped from the classical definition. This is done in order to have a symmetric (but not positive-definite) system of equations rather than a non-symmetric (but positive-definite) system of equations.
A typical set of boundary conditions on the boundary \(\partial \Omega = \Gamma_{D} \cup \Gamma_{N}\) can be:
21.1.2. Weak formulation¶
The Stokes equations can easily be formulated in a mixed variational form; that is, a form where the two variables, the velocity and the pressure, are approximated simultaneously. Using the abstract framework, we have the problem: find \((u, p) \in W\) such that
for all \((v, q) \in W\), where
The space \(W\) should be a mixed (product) function space \(W = V \times Q\), such that \(u \in V\) and \(q \in Q\).
21.1.3. Domain and boundary conditions¶
In this demo, we shall consider the following definitions of the input functions, the domain, and the boundaries:
- \(\Omega = [0,1]\times[0,1] \backslash {\rm dolphin}\) (a unit cube)
- \(\Gamma_D =\)
- \(\Gamma_N =\)
- \(u_0 = (- \sin(\pi x_1), 0.0)\) for \(x_0 = 1\) and \(u_0 = (0.0, 0.0)\) otherwise
- \(f = (0.0, 0.0)\)
- \(g = (0.0, 0.0)\)
21.2. Implementation¶
First, the dolfin module is imported:
from dolfin import *
In this example, different boundary conditions are prescribed on
different parts of the boundaries. This information must be made
available to the solver. One way of doing this, is to tag the
different sub-regions with different (integer) labels. DOLFIN provides
a class MeshFunction which
is useful for these types of operations: instances of this class
represent functions over mesh entities (such as over cells or over
facets). Mesh and mesh functions can be read from file in the
following way:
# Load mesh and subdomains
mesh = Mesh("dolfin_fine.xml.gz")
sub_domains = MeshFunction("size_t", mesh, "dolfin_fine_subdomains.xml.gz")
Next, we define a MixedFunctionSpace composed of a
VectorFunctionSpace of continuous
piecewise quadratics and a FunctionSpace of continuous piecewise
linears. (This mixed finite element space is known as the Taylor–Hood
elements and is a stable, standard element pair for the Stokes
equations.)
# Define function spaces
V = VectorFunctionSpace(mesh, "CG", 2)
Q = FunctionSpace(mesh, "CG", 1)
W = V * Q
Now that we have our mixed function space and marked subdomains defining the boundaries, we define boundary conditions:
# No-slip boundary condition for velocity
# x1 = 0, x1 = 1 and around dolphin
noslip = Constant((0, 0))
bc0 = DirichletBC(W.sub(0), noslip, sub_domains, 0)
# Inflow boundary condition for velocity
# x0 = 1
inflow = Expression(("-sin(x[1]*pi)", "0.0"))
bc1 = DirichletBC(W.sub(0), inflow, sub_domains, 1)
# Boundary condition for pressure at outflow
# x0 = 0
zero = Constant(0)
bc2 = DirichletBC(W.sub(1), zero, sub_domains, 2)
# Collect boundary conditions
bcs = [bc0, bc1, bc2]
Here, we have given four arguments in the call to
DirichletBC. The first
specifies the FunctionSpace. Since we have a
MixedFunctionSpace, we write
W.sub(0) for the function space V, and W.sub(1) for
Q. The second argument specifies the value on the Dirichlet
boundary. The two last ones specifies the marking of the subdomains;
sub_domains contains the subdomain markers and the number given as
the last argument is the subdomain index.
The bilinear and linear forms corresponding to the weak mixed formulation of the Stokes equations are defined as follows:
# Define variational problem
(u, p) = TrialFunctions(W)
(v, q) = TestFunctions(W)
f = Constant((0, 0))
a = (inner(grad(u), grad(v)) - div(v)*p + q*div(u))*dx
L = inner(f, v)*dx
To compute the solution we use the bilinear and linear forms, and the
boundary condition, but we also need to create a Function to store the solution(s). The (full)
solution will be stored in w, which we initialize using the
MixedFunctionSpace W. The actual
computation is performed by calling solve with the arguments a,
L, w and bcs. The separate components u and p of
the solution can be extracted by calling the split function. Here we use an
optional argument True in the split function to specify that we want a
deep copy. If no argument is given we will get a shallow copy. We want
a deep copy for further computations on the coefficient vectors.
# Compute solution
w = Function(W)
solve(a == L, w, bcs)
# Split the mixed solution using deepcopy
# (needed for further computation on coefficient vector)
(u, p) = w.split(True)
We may be interested in the \(L^2\) norms of u and p, they can be calculated and printed by writing
print "Norm of velocity coefficient vector: %.15g" % u.vector().norm("l2")
print "Norm of pressure coefficient vector: %.15g" % p.vector().norm("l2")
One can also split functions using shallow copies (which is enough when we just plotting the result) by writing
# Split the mixed solution using a shallow copy
(u, p) = w.split()
Finally, we can store to file and plot the solutions.
# Save solution in VTK format
ufile_pvd = File("velocity.pvd")
ufile_pvd << u
pfile_pvd = File("pressure.pvd")
pfile_pvd << p
# Plot solution
plot(u)
plot(p)
interactive()
21.3. Complete code¶
from dolfin import *
# Load mesh and subdomains
mesh = Mesh("../dolfin_fine.xml.gz")
sub_domains = MeshFunction("size_t", mesh, "../dolfin_fine_subdomains.xml.gz")
plot(mesh)
plot(sub_domains)
# Define function spaces
V = VectorFunctionSpace(mesh, "CG", 2)
Q = FunctionSpace(mesh, "CG", 1)
W = V * Q
# No-slip boundary condition for velocity
# x1 = 0, x1 = 1 and around the dolphin
noslip = Constant((0, 0))
bc0 = DirichletBC(W.sub(0), noslip, sub_domains, 0)
# Inflow boundary condition for velocity
# x0 = 1
inflow = Expression(("-sin(x[1]*pi)", "0.0"))
bc1 = DirichletBC(W.sub(0), inflow, sub_domains, 1)
# Boundary condition for pressure at outflow
# x0 = 0
zero = Constant(0)
bc2 = DirichletBC(W.sub(1), zero, sub_domains, 2)
# Collect boundary conditions
bcs = [bc0, bc1, bc2]
# Define variational problem
(u, p) = TrialFunctions(W)
(v, q) = TestFunctions(W)
f = Constant((0, 0))
a = (inner(grad(u), grad(v)) - div(v)*p + q*div(u))*dx
L = inner(f, v)*dx
# Compute solution
w = Function(W)
solve(a == L, w, bcs)
# Split the mixed solution using deepcopy
# (needed for further computation on coefficient vector)
(u, p) = w.split(True)
print "Norm of velocity coefficient vector: %.15g" % u.vector().norm("l2")
print "Norm of pressure coefficient vector: %.15g" % p.vector().norm("l2")
# # Split the mixed solution using a shallow copy
(u, p) = w.split()
# Save solution in VTK format
ufile_pvd = File("velocity.pvd")
ufile_pvd << u
pfile_pvd = File("pressure.pvd")
pfile_pvd << p
# Plot solution
plot(u)
plot(p)
interactive()