How can I "plot" the stress tensor over a mesh in solid mechanics?

Question

cf. Ch. 26 Applications in Solid Mechanics, FEniCS book

First, let me point out my python script linelast01.py in my github repository SME:

https://github.com/ernestyalumni/SME/blob/master/linelast01.py

as I’ve implemented linear elasticity for the BoxMesh: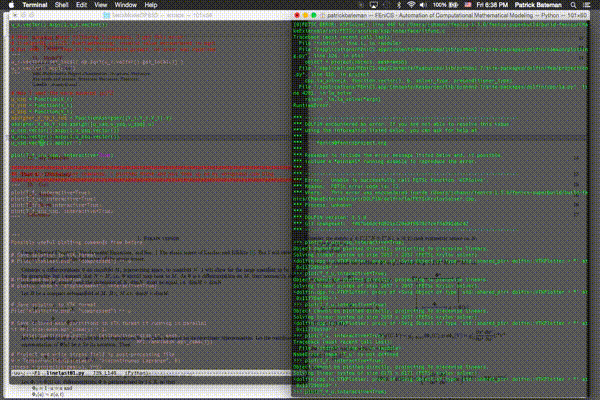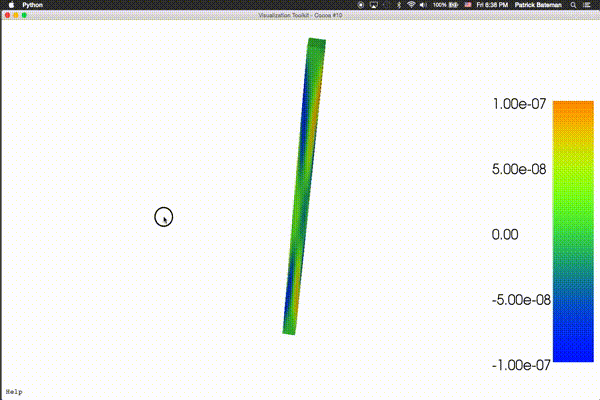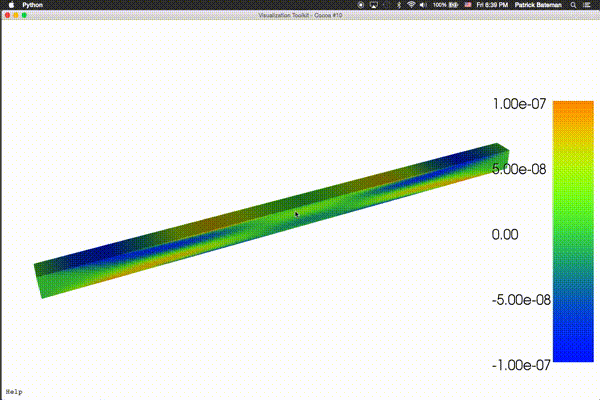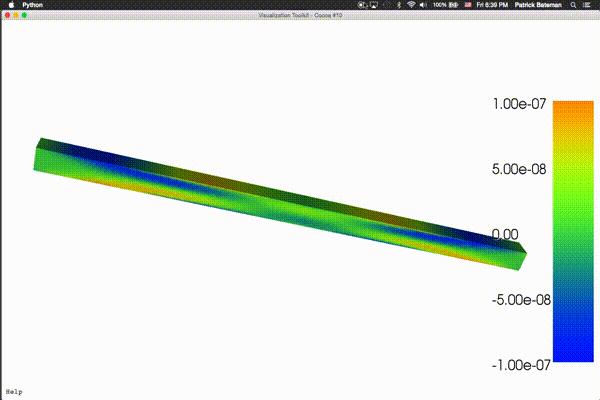

To the point, I was able to successfully calculate the displacement $u$ with LinearVariationalSolver for my solid mechanics problem. $u$ is a vector valued function Function(V) over the mesh. V = VectorFunctionSpace(mesh,’Lagrange’,2). What I can get is the stress tensor, a rank-2 symmetric tensor, with

sigma_f = 2musym(grad(u)) + lmbdatr(grad(u))Identity(3)

from the displacement u, after having solved u.

But what can I do to "plot" the stress tensor over the mesh? Should I multiply it with the displacement u to get something sensible to try to understand and make sense of the stress tensor? Is there something else I could multiply the stress tensor, other than the FacetNormal, say the unit vector field in the x direction, to get the different stress tensor entries over the mesh?

What I have so far is that I multiplied the stress tensor with the displacement, and again, with the displacement:

https://youtu.be/gkUTYqBP7JA

https://youtu.be/tvbV7v8IDkc

I want to make sense of what this means physically: does it make sense to say that this is the force, due to the displacement, at each point of the mesh, and the magnitude of the force, due to the displacement, in the direction of the displacement, respectively? What if I want to get just the pressure at each point of the mesh, due to this stress tensor? Should I somehow just get a surface area on the surface of my BoxMesh and “multiply” that with this stress tensor? How can I implement that in FEniCS?

Answer 1

Hello,

as you already noticed, the stress is a 9-dimensional variable (6 if you count symmetry), which is hard to plot. So you need some 1 dimensional variable, which is a "good" summary of the stress tensor at each point.

What "good" really means, depends on what you want to know and what type of
material you are using.

I don't really know if what you calculated has any physical meaning, though. What you want to plot, is probably something like the "load" that each point experiences. A good place to start in that case would be to plot something like the maximum eigenvalue of the stress-tensor at each point.

Other than that, there are many quantities that engineers use to calculate the "actual stress" at a point, for example when trying to determine whether or not the load at a point is larger than some critical value. The "von-mises yield criterion" is one example. https://en.wikipedia.org/wiki/Von_Mises_yield_criterion . What you want is the formula with the large "sqaure root" just below the the heading "reduced von mises equation.... "

Maybe we should first figure out what you want to plot and then have a look at how to implement it.

regards

Comments

@multigrid202 The eigenvalue and von-mises suggestions are very helpful; frankly, I needed to know what "keywords" to look up and go from there; I'll try to report what I find out in a week or so; thanks! Let us know if you have any other thoughts.

---

The trace of the eigenvalues seem to be 1 quantity to possibly plot. Hopefully I could find how to get the eigenvalues at each point in the FeniCS book; let me know if any of you guys had a specific reference.

---

I would try to convert the stress tensor into numpy arrays and then take it from there. If u is a scalarfunction, then the proper command would be u_array = u.vector().array(). Because the stress is matrix-valued, you probably have to use a split() first and then combine the scalar components of the stress to form a numpy array.

---

I think the following is helpful:
http://fenicsproject.org/qa/1488/plot-my-stress-tensor-components