I am interesting in solving the following nonlinear, time-dependent pde in 2 spatial dimensions:
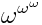
The goal is to find steady state solutions for the function $\psi$, for different parameters $\sigma$. Here $\sigma$ is a positive real-valued parameter. The boundary conditions can initially be of the Dirichlet type, setting the function $\psi$ to zero on the contour of a square, but later on I plan to implement some absorbing BC (perhaps using the perfectly matched layer method?).
For the time-dependence, I plan to use the Gryphon module of Erik Skare (https://launchpad.net/gryphonproject), which is basically a Runge-Kutta solver and for the spatial part Fenics.
So the question is, do you think this is feasible to do with Fenics, and if so, what are more or less the steps one has to follow?