Coupling two scalar fields yielding in a Dirichilet BC expecting a vector function.

Question

Dear all,
I have been trying to solve the following coupled problem:

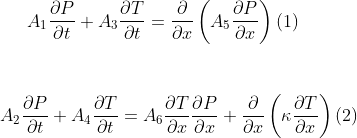
T is the temperature, P is the pressure, I am trying to solve in 1D first.

---

I have a robin boundary condition for both boundaries at the sides for pressure.
For the temperature I have a Dirichilet boundary condition and a Robin condition at the opposite side.
However I have 2 major doubts. The first one is that I am trying to define the function space for my two scalar functions:

P1 = FiniteElement('P', interval , 1)
V = FunctionSpace(mesh, MixedElement([P1,P1]))
u = Function(V)

However, when trying to define the Dirichilet Boundary Condition,

T_D = Expression('t + 120.0', degree=2, t=0)
bcl_T = 'near(x[0],0)'
bc = DirichletBC(V, T_D, bcl_T)

I get the following error:

*** Error:   Unable to create Dirichlet boundary condition.
*** Reason:  Expecting a vector-valued boundary value but given function is scalar.
*** Where:   This error was encountered inside DirichletBC.cpp.

I think I don't understand what I am doing with a MixedElement, I thought I would have a function space for both my scalar functions (Temperature T and Pressure P).

I am also in doubt of how to develop the variational formulation.
I have put equations 1 and 2 in their weak form, I supose I have to use different test functions and sum them.
As they are nonlinear, I would solve F == 0, where F would be the sum of both weak forms of equations 1 and 2.
Am I right?

Thank you for your attention, evryone here is really helpful.
All the best, Murilo.

Comments

What is T_D? You can specify separate boundary conditions for T and P by using V.sub(0)and V.sub(1). If T_D is a scalar, try to make it into a vector, e.g T_D = Constant((T0, P0))

---

Dear Fisberg, sorry I am an idiot and left one of the most important parts out.
As I add to the question, T_D is an expression that I use to simulate a heating on this side. t is the time that I update, on my loop.

T_D = Expression('t + 120.0', degree=2, t=0)

Do you think I can make this function a vector?

Thank you for your quick response and sorry for the lack of attention on my question.
All the best, Murilo.

---

Yes, you should make this function into a vector, e.g

T_D = Expression(('expression for T', 'expression for P'), degree=2, t = 0)

---

Nice! But in case I don't have a expression for P (I mean, I don't want a Dirichilet Boundary at this position) do you know how should I proceed?
Thank you for your time!

---

Then you substitute V with V.sub(0) (or V.sub(1)depending on wether T is in the first or second subspace)

---

Dear Finsberg,
I tried to implement and the answer was easier then I thought!
As you said, using the V.sub(0) as the space for the Dirichlet boundary condition was enough to solve the problem!
Thank you very much for your help! However, now I am facing a new issue.
I am trying to interpolate a constant as a initial condition for my solution, eg. initial temperature f 20. I am trying this:

T_0 = Constant('20')
T_n = interpolate(T_0, V(0)) 

However I got this error:

*** Error: Unable to create function.
*** Reason: Cannot be create from subspace. Consider collapsing function space.

Do you have any idea of how to solve this issue?
Thank you very much for all your help!

EDIT:
After a quick search I found the answer!
Significance of collapsing
I will not close yet since I will wait to see if anybody can help with the functional doubts.
Thank you!

Answer 1

Restrict boundary condition to a subspace:

bc = DirichletBC(V.sub(0), T_D, bcl_T)

Interpolate a constant into a subspace:

T_n = interpolate(T_0, V.sub(0).collapse())

Comments

Dear finsberg,
Perfect! Now everybody with similar doubts can understand how to make it right.
Thank you!
All the best, Murilo.