Built-in meshes

This demo is implemented in a single Python file, demo_built-in-meshes.py, and demonstrates use of the built-in meshes in DOLFIN.

This demo illustrates:

• How to define some of the different built-in meshes in DOLFIN

Problem definition

The demo focuses on the built-in meshes. We will look at the following meshes:

• UnitIntervalMesh

• UnitSquareMesh

• RectangleMesh

• UnitCubeMesh

• BoxMesh

Implementation

First, the dolfin module is imported:

from dolfin import *
import matplotlib.pyplot as plt

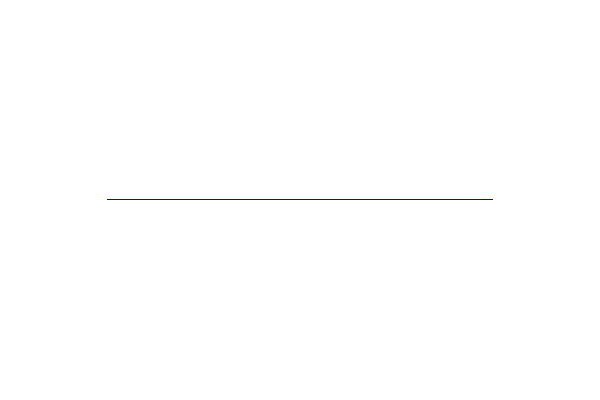
The first mesh we make is a mesh over the unit interval \((0,1)\). UnitIntervalMesh takes the number of intervals \((n_x)\) as input argument, and the total number of vertices is therefore \((n_x+1)\).

mesh = UnitIntervalMesh(10)
print("Plotting a UnitIntervalMesh")
plt.figure()
plot(mesh, title="Unit interval")

This produces a mesh looking as follows:

We then make our first version of a mesh on the unit square \([0,1] \times [0,1]\). We must give the number of cells in the horizontal and vertical directions as the first two arguments to UnitSquareMesh. There is a third optional argument that indicates the direction of the diagonals. This can be set to “left”, “right”, “right/left”, “left/right”, or “crossed”. We can also omit this argument and thereby use the default direction “right”.

mesh = UnitSquareMesh(10, 10)
print("Plotting a UnitSquareMesh")
plt.figure()
plot(mesh, title="Unit square")

Our second version of a mesh on the unit square has diagonals to the left, the third version has crossed diagonals and our final version has diagonals to both left and right:

mesh = UnitSquareMesh(10, 10, "left")
print("Plotting a UnitSquareMesh")
plot(mesh, title="Unit square (left)")

mesh = UnitSquareMesh(10, 10, "crossed")
print("Plotting a UnitSquareMesh")
plot(mesh, title="Unit square (crossed)")

mesh = UnitSquareMesh(10, 10, "right/left")
print("Plotting a UnitSquareMesh")
plt.figure()
plot(mesh, title="Unit square (right/left)")

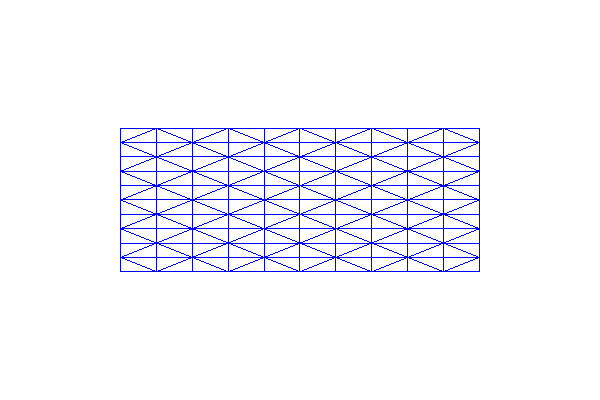
The class RectangleMesh creates a mesh of a 2D rectangle spanned by two points (opposing corners) of the rectangle. Three additional arguments specify the number of divisions in the \(x\)- and \(y\)-directions, and as above the direction of the diagonals is given as a final optional argument (“left”, “right”, “left/right”, or “crossed”). In the first mesh we use the default direction (“right”) of the diagonal, and in the second mesh we use diagonals to both left and right.

mesh = RectangleMesh(Point(0.0, 0.0), Point(10.0, 4.0), 10, 10)
print("Plotting a RectangleMesh")
plt.figure()
plot(mesh, title="Rectangle")

mesh = RectangleMesh(Point(-3.0, 2.0), Point(7.0, 6.0), 10, 10, "right/left")
print("Plotting a RectangleMesh")
plt.figure()
plot(mesh, title="Rectangle (right/left)")

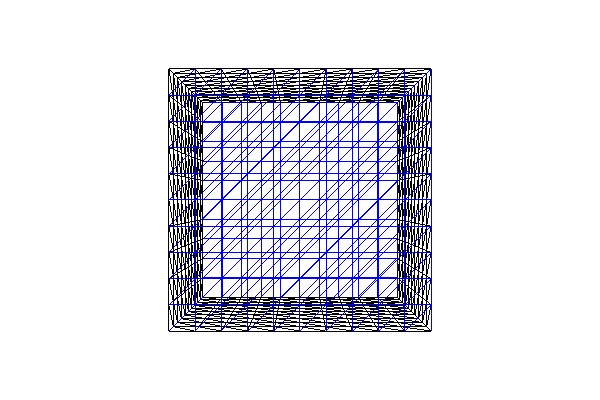
To make a mesh of the 3D unit cube \([0,1] \times [0,1] \times [0,1]\), we use UnitCubeMesh. UnitCubeMesh takes the number of cells in the \(x\)-, \(y\)- and \(z\)-direction as the only three arguments.

mesh = UnitCubeMesh(10, 10, 10)
print("Plotting a UnitCubeMesh")
plt.figure()
plot(mesh, title="Unit cube")

Finally we will demonstrate a mesh on a rectangular prism in 3D. The prism is specified by two points (opposing corners) of the prism. Three additional arguments specify the number of divisions in the \(x\)-, \(y\)- and \(z\)-directions.

Meshes for more complex geometries may be created using the mshr library, which functions as a plugin to DOLFIN, providing support for Constructive Solid Geometry (CSG) and mesh generation. For more details, refer to the mshr documentation.

mesh = BoxMesh(Point(0.0, 0.0, 0.0), Point(10.0, 4.0, 2.0), 10, 10, 10)
print("Plotting a BoxMesh")
plt.figure()
plot(mesh, title="Box")
plt.show()